Hardy and Weinberg worked on a  mathematical approach to population genetics and the results of their work predict that overtime in a gene pool that is closed and allows for the random mating of individuals within the populations the frequency of the genes that make up the gene pool will remain constant.
This begs the question of how does evolution proceed in the face of this prediction???

Let's recall the Punnet Square

The mating of  two black mice  individuals that are heterozygous (e.g., Bb) for a trait, we find that
B= black hair b = white hair

• 25% of their offspring are homozygous for the dominant allele (BB) (Black Hair)
• 50% are heterozygous like their parents (Bb)  (Black Hair)
• 25% are homozygous for the recessive allele (bb) and thus, unlike their parents, express the recessive phenotype. (White Hair)

• meiosis separates the two alleles of each heterozygous parent so that 50% of the gametes will carry one allele and 50% the other.
• gametes conceive at random, each B or b -carrying ovum  will have a 1 in 2 probability of being fertilized by a sperm carrying B or b. (see above)

But the frequency of two alleles in an entire population of organisms is unlikely to be exactly the same. In a population of mice in which

• 80% of all the gametes in the population carry a dominant allele for black coat (B) and
• 20% carry the recessive allele for white coat (b).

Random union of these gametes (right table) will produce a generation:

• 64% homozygous for BB (0.8 x 0.8 = 0.64)
• 32% Bb heterozygotes (0.8 x 0.2 x 2 = 0.32)
• 4% homozygous (bb) for white coat (0.2 x 0.2 = 0.04)

So 96% of this generation will have black coats; only 4% white coats.
Do white coated mice eventually vanish (assuming there is external selective force)?

No!

• All the gametes formed by BB mice will contain allele B as will
• one-half the gametes formed by heterozygous (Bb) mice.
• So, 80% (0.64 + .5*0.32) of the pool of gametes formed by this generation with contain B.

• All the gametes of the white (bb) mice (4%) will posses b but .....
• one-half of the gametes of the heterozygous mice will as well.
• So 20% (0.04 + .5*0.32) of the gametes will contain b.

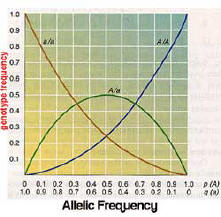
Thus we have come back to the original condition. The frequency of allele b in the population is the same as before. The heterozygous mice ensure that each generation will contain 4% white mice.

Next , we look at an algebraic analysis of the same problem using  expansion of the binomial (p+q)².

(p+q)² = p² + 2pq + q²

• The total number of genes in a population is its gene pool.
• Let p represent the frequency of one gene in the pool and q the frequency of its single allele.
• So, p + q = 1
  • p² = the fraction of the population homozygous for p
  • q² = the fraction homozygous for q
  • 2pq = the fraction of heterozygotes
• In our example, p = 0.8, q = 0.2, and thus

  (0.8 + 0.2)² = (0.8)² + 2(0.8)(0.2) + (0.2)² = 064 + 0.32 + 0.04

The algebraic method enables us to work backward as well as forward. In fact, because we chose to make B fully dominant, the only way that the frequency of B and b in the gene pool could be known is by determining the frequency of the recessive phenotype (white) and computing from it the value of q.

q² = 0.04, so q = 0.2, the frequency of the b allele in the gene pool. Since p + q = 1, p = 0.8 and allele B makes up 80% of the gene pool. Because B is completely dominant over b, we cannot distinguish the Bb mice from the BB ones by their phenotype. Substituting in the middle term (2pq) of the expansion gives the percentage of heterozygous mice. 2pq = (2)(0.8)(0.2) = 0.32

Thus we find recessive genes do not tend to be lost from a population .

gene frequencies and genotype ratios in a randomly-breeding population remain constant from generation to generation.

This is known as the Hardy-Weinberg law in honor of the two men who first realized the significance of the binomial expansion to population genetics and hence to evolution.

Evolution involves changes in the gene pool.
 A population in Hardy-Weinberg equilibrium shows no change.
What the law tells us is that populations are able to maintain a reservoir of variability so that if future conditions require it, the gene pool can change.
If recessive alleles were continually tending to disappear, the population would soon become homozygous.
Hardy and Weinberg suggest, genes that have no present selective value (recessive) will persist through time. Diversity is preserved.

So what is it that drives evolution then if stability of the gene pool of a population is the norm? Stay tuned and we shall see.